计组虐我千百遍~
在这里,我将梳理教材 (数字逻辑概论[9787301343692]) 各个章节内容,尽可能得浅显易懂
计算机组成原理-数字逻辑概论
Number System and Codes
-
Number Systems
- 数制中我们常用的有十进制(Decimal)、二进制(Binary)、十六进制(Hexadecimal)、八进制(Octal)
-
Number Conversion
- 在k进制下,数的实际大小 \(S_k=\sum_{i=-n}^{m-1} a_i \times k^i (a_i \in \{0, 1, 2, \ldots, k-1\})\)
- 例如: \((2A.3)_{16} = 2 \times 16^1 + 10 \times 16^0 + 3 \times 16^{-1} = 32 + 10 + 0.1875 = (42.1875)_{10}\)
- LSB (Least Significant Bit) 最低有效位、MSB (Most Significant Bit) 最高有效位,在大端模式中MSB先传输,小端模式中LSB先传输
- Signed Binary Numbers
- Signed-Magnitude(原码)
- 添加0或1在MSB前,表示正负
- 其余位正常表示数值大小
- 例如: \(+5 = [0101]_{SM}\) , \(-5 = [1101]_{SM}\) , \(-0=[10..0]_{SM}\)
- 范围: \(-(2^{n-1}-1)\) 到 \(+(2^{n-1}-1)\)
- Ones’ Complement(反码)
- 当数值为负,所有位反转并在前添1,当数值为正,直接添0
- 例如: \(+5 = [0101]_{OC}\) , \(-5 = [1010]_{OC}\) , \(-0=[11..1]_{OC}\)
- 范围: \(-(2^{n-1}-1)\) 到 \(+(2^{n-1}-1)\)
- 优点:加减法运算统一,可直接由原码转换
- 注意:存在两个零表示(+0和-0)
- Twos’ Complement(补码)
- 当数值为负,先取反码再加1;当数值为正,直接添0
- 例如: \(+5 = [0101]_{TC}\) , \(-5 = [1011]_{TC}\) , \(+0=[00..0]_{TC}\)
- 范围: \(-2^{n-1}\) 到 \(+(2^{n-1}-1)\)
- 优点:只有一个零表示,加减法运算统一
- 计算规律:负数的补码 = 原码取反 + 1,或者从右往左第一个1保持不变,其余位取反
- Signed-Magnitude(原码)
- Addition and Subtraction of Signed Binary Numbers
- 对SM来说,计算可以先肉眼观察哪个绝对值更大,然后再让另一个与其做运算。
- 对OC来说,加减法运算是统一的,都可以无论加减都转换成加,再做正常二进制加法,并把最高位循环进位加给最低位即可。
- 对TC来说,加减法运算是统一的,直接做正常二进制加法,最简单。
- Numerical Codes
- Binary Coded Decimal(BCD)
- 8421Code
- Excess-3Code(余三码)具有自补性
- 5421Code
- 自补性(Self-Complementing Property):编码满足: 编码(9-n) = 编码(n)的按位取反
Dec 8421 Excess-3 5421 0 0000 0011 0000 1 0001 0100 0001 2 0010 0101 0010 3 0011 0110 0011 4 0100 0111 0100 5 0101 1000 1000 6 0110 1001 1001 7 0111 1010 1010 8 1000 1011 1011 9 1001 1100 1100 - Gray Code(格雷码)
- 具有相邻数值只有一位编码不同的优越特性,有效避免多位跳变,提高系统可靠性。
- 二进制转格雷码:
- \(G_{n-1} = B_{n-1}\) (最高位相同)
- \(G_i = B_{i+1} ⊕ B_i\) (其他位为高位二进制与当前位异或)
- Parity Code(奇偶校验码)
- Odd Parity(奇校验)
- 检验位设置使得整个码字中的1的个数为奇数
- Even Parity(偶校验)
- 校验位设置使得整个码字中的1的个数为偶数
- 只能检测奇数个bit错误
Logical Algebra
- Odd Parity(奇校验)
- Binary Coded Decimal(BCD)
- Three Basic Function of Logical Algebra
- AND
- OR
- NOT
- 过于简单不详述
- Laws and Rules of Logical Algebra
布尔代数基本定律
- 交换律 (Commutative Laws) - $$ A + B = B + A $$ - $$ A · B = B · A $$ - 结合律 (Associative Laws) - $$ A + (B + C) = (A + B) + C $$ - $$ A · (B · C) = (A · B) · C $$ - 分配律 (Distributive Laws) - $$ A · (B + C) = A · B + A · C $$ - $$ A + (B · C) = (A + B) · (A + C) $$ - 互补律 (Complement Laws) - $$ A + \overline{A} = 1 $$ - $$ A · \overline{A} = 0 $$ - 同一律 (Identity Laws) - $$ A + 0 = A $$ - $$ A · 1 = A $$ - 零元律 (Null Laws) - $$ A + 1 = 1 $$ - $$ A · 0 = 0 $$ - 重复律 (Idempotent Laws) - $$ A + A = A $$ - $$ A · A = A $$ - 吸收律 (Absorption Laws) - $$ A + A · B = A $$ - $$ A · (A + B) = A $$ - 反演律 (Involution Law) - $$ \overline{\overline{A}} = A $$ - **德摩根定律** (De Morgan's Laws) - $$ \overline{A+B} = \overline{A} · \overline{B} $$ - $$ \overline{A · B} = \overline{A} + \overline{B} $$ - **一致律** (Consensus Laws) - $$ A · B + \overline{A} · C + B · C = A · B + \overline{A} · C $$ - $$ (A + B) · (\overline{A} + C) · (B + C) = (A + B) · (\overline{A} + C) $$ - **冗余律** (Redundancy Laws) - $$ A + \overline{A} · B = A + B $$ - $$ A · (\overline{A} + B) = A · B $$- Duality Rule (对偶规则)
- 定义:将布尔表达式中的 + 与 ·,0 与 1 互换,变量不变,得到对偶式
- 重要性质:如果一个布尔等式成立,其对偶式也必然成立
- 示例: \(F_1=A+B·C\) , \(F_2=(A+B)·(A+C)\) ,有 \(F_1^D=A·(B+C)=A·B+A·C=F_2^D\) ,故 \(F_1=F_2\)
- Expansion Rule (Shannon’s Expansion Theorem)
-
基本形式:对于任意布尔函数 \(F(x_1, x_2, \ldots, x_n)\) ,可以按照变量 \(x_i\) 进行展开:\(F(x_1, x_2, \ldots, x_n) = x_i \cdot F(x_1, \ldots, x_{i-1}, 1, x_{i+1}, \ldots, x_n) + \overline{x_i} \cdot F(x_1, \ldots, x_{i-1}, 0, x_{i+1}, \ldots, x_n)\)
-
递归展开:可以对多个变量连续展开 \(F(A,B,C) = A \cdot F(1,B,C) + \overline{A} \cdot F(0,B,C)\) \(= A \cdot [B \cdot F(1,1,C) + \overline{B} \cdot F(1,0,C)] + \overline{A} \cdot [B \cdot F(0,1,C) + \overline{B} \cdot F(0,0,C)]\)
-
- 异或同或
- 异或与同或满足分配律和交换律
- 异或与同或的零一律很特殊
- \[A ⊕ 0 = A\]
- \[A ⊕ 1 = \overline{A}\]
- \[A ⊙ 0 = \overline{A}\]
- \[A ⊙ 1 = A\]
- Duality Rule (对偶规则)
- Function Transformation
- Standard Froms
- Canonical AND-OR
- Minterm(极小项)
- 定义:n个变量的最小项是包含所有n个变量的乘积项,每个变量以原变量或反变量形式出现且仅出现一次
-
特性:在2ⁿ种变量组合中,每个最小项仅在一种组合下为1,其余均为0
A B C Minterm 0 0 0 m₀ = Ā·B̄·C̄ 0 0 1 m₁ = Ā·B̄·C 0 1 0 m₂ = Ā·B·C̄ 0 1 1 m₃ = Ā·B·C 1 0 0 m₄ = A·B̄·C̄ 1 0 1 m₅ = A·B̄·C 1 1 0 m₆ = A·B·C̄ 1 1 1 m₇ = A·B·C
- Canonical OR-AND
- Maxterm(极大项)
- 定义:n个变量的最大项是包含所有n个变量的加法项,每个变量以原变量或反变量形式出现且仅出现一次
- 特性:在2ⁿ种变量组合中,每个最大项仅在一种组合下为0,其余均为1
A B C Maxterm 0 0 0 M₀ = A+B+C 0 0 1 M₁ = A+B+C̄ 0 1 0 M₂ = A+B̄+C 0 1 1 M₃ = A+B̄+C̄ 1 0 0 M₄ = Ā+B+C 1 0 1 M₅ = Ā+B+C̄ 1 1 0 M₆ = Ā+B̄+C 1 1 1 M₇ = Ā+B̄+C̄ - 互补关系:Mᵢ = m̄ᵢ(第i个最大项等于第i个最小项的反)
- 德摩根转换:
- 如果 F = Σm(1,3,5,7),则 F = ΠM(0,2,4,6)
- 即不在最小项列表中的项构成最大项列表
- 因此这类题其实做真值表非常显然
- Maxterm(极大项)
- Minterm(极小项)
- 逻辑相邻(Logical Adjacency):在布尔运算中,只有当两个形式中只有一个变量不同时才被称作相邻
-
例题
Wirte the sum of Minterms of a function - $$ F(A,B,C)=\overline{(A\overline{B}+B\overline{C})\overline{AB}} $$解答过程
- **Step 1: 化简原函数** - $$ F(A,B,C) = \overline{(A\overline{B}+B\overline{C})\overline{AB}} \\ = \overline{(A\overline{B}+B\overline{C})} + \overline{\overline{AB}} \\ = \overline{(A\overline{B}+B\overline{C})} + AB \\ = \overline{A\overline{B}} \cdot \overline{B\overline{C}} + AB \\ = (\overline{A}+B) \cdot (\overline{B}+C) + AB $$ - **Step 2: 展开分配律** $$ = \overline{A}\overline{B} + \overline{A}C + B\overline{B} + BC + AB \\ = \overline{A}\overline{B} + \overline{A}C + BC + AB $$ - **Step 3: 补全变量(恢复缺失变量)** $$ \\ \overline{A}\overline{B} = \overline{A}\overline{B}(C + \overline{C}) = \overline{A}\overline{B}C + \overline{A}\overline{B}\overline{C} \\ \overline{A}C = \overline{A}C(B + \overline{B}) = \overline{A}BC + \overline{A}\overline{B}C \\ BC = BC(A + \overline{A}) = ABC + \overline{A}BC \\ AB = AB(C + \overline{C}) = ABC + AB\overline{C} $$ - **Step 4: 合并同类项** $$ F = \overline{A}\overline{B}\overline{C} + \overline{A}\overline{B}C + \overline{A}BC + AB\overline{C} + ABC $$ - **Step 5: 识别最小项** $$ \\ \overline{A}\overline{B}\overline{C} → 000 → m_0 \\ \overline{A}\overline{B}C → 001 → m_1 \\ \overline{A}BC → 011 → m_3 \\ AB\overline{C} → 110 → m_6 \\ ABC → 111 → m_7 - **最终答案**: $$ F = m_0 + m_1 + m_3 + m_6 + m_7 = \sum m(0,1,3,6,7) $$
</details>
- Function Simplification
- Simplest function
- 定义:项数最少,每一项中的变量也最少的表达形式
-
例题
Write the simplification of AND-OR functions - $$ F(A,B,C,D,E) = AC + \overline{B}C + B\overline{D} + C\overline{D} + A(B + \overline{C}) + \overline{A}BC\overline{D} + A\overline{B}DE $$**tips** :对于化为最简OR-AND形式的题,可以采用对偶求得AND-OR形式再对偶求得。答案
$$ F=A+\overline{B}C+B\overline{D} $$
</details>
- K-Map(卡诺图\烧烤图)
- 卡诺图是一种图形化的布尔函数化简方法,通过格雷码排列的方式将逻辑相邻的最小项放在物理相邻的位置。
-
4变量K-Map (当变量大于5时难以构造,故一般只用到4变量)
CD=00 CD=01 CD=11 CD=10 AB=00 m₀ m₁ m₃ m₂ AB=01 m₄ m₅ m₇ m₆ AB=11 m₁₂ m₁₃ m₁₅ m₁₄ AB=10 m₈ m₉ m₁₁ m₁₀ - 化简规则
- 基本原则: \(AB + A\overline{B} = A\) (消去不同的变量)
- 圈的要求:
- 圈的大小必须是2的幂次:1, 2, 4, 8, 16…
- 圈必须是矩形(包括正方形)
- 圈应尽可能大,以获得最大化简
- 所有为1的格子都必须被圈覆盖
- 圈可以重叠
- 利用卡诺图的环形特性,边界可以相连
- Don’t Care条件
- 用X或d表示,表示该状态下函数值无关紧要
- 在化简时可以将X当作0或1使用,以获得最佳化简效果
- 最终结果中X可以是0也可以是1
-
例题
Use K-Map to simplify the following functions - $$ F(A,B,C,D) = \sum m(0,1,4,5,6,7,8,9,11,15) $$解答过程
- **Step 1: 画出4变量卡诺图并填入1**(对于M则是0) | | CD=00 | CD=01 | CD=11 | CD=10 | |:---:|:-----:|:-----:|:-----:|:-----:| |AB=00| 1 | 1 | 0 | 0 | |AB=01| 1 | 1 | 1 | 1 | |AB=11| 0 | 0 | 1 | 0 | |AB=10| 1 | 1 | 1 | 0 | - **Step 2: 寻找可圈的矩形** - 圈1:m₀,m₁,m₄,m₅ (2×2矩形) → $$ \overline{A}\overline{C} $$ - 圈2:m₄,m₅,m₆,m₇ (1×4矩形) → $$ A\overline{B} $$ - 圈3:m₈,m₉,m₁₁ 需要与边界m₁₅连接 → $$ B\overline{C}\overline{D} + BC\overline{D} + B\overline{C}D + BCD $$ - **Step 3: 重新分析找最优解** - 圈1:m₀,m₁,m₄,m₅ → $$ \overline{C}\overline{D} $$ - 圈2:m₄,m₅,m₆,m₇ → $$ A\overline{B} $$ - 圈3:m₈,m₉ → $$ B\overline{A}\overline{C} $$ - 圈4:m₁₁,m₁₅ → $$ BCD $$ - **最终答案**: $$F = \overline{C}\overline{D} + A\overline{B} + B\overline{A}\overline{C} + BCD $$
</details>
- Simplest function
Digital Circuit
- CMOS Transistor
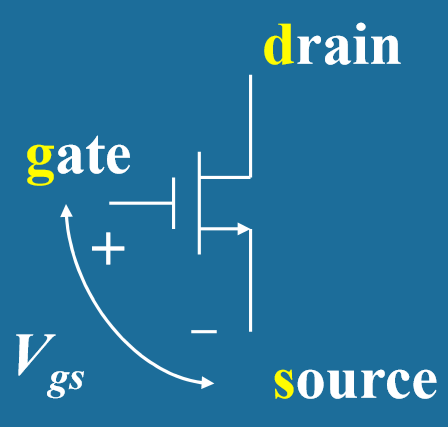
- NMOS晶体管 (N-channel Metal-Oxide-Semiconductor)
- 结构组成:包含gate(栅极)、source(源极)、drain(漏极)三个端子
- 工作原理:通过栅极电压( Vgs )控制source-drain之间的电阻( Rds ),起到逻辑控制开关的作用
- 开关特性:
- 当 Vgs = 0 时:NMOS晶体管处于OFF状态, Rds 很大( > 106Ω )
- 当 Vgs > 0 (高电平)时:NMOS晶体管处于ON状态, Rds 显著降低
- 控制规律: Vgs 增大 → Rds 减小 (Not point in - 非反向导通)
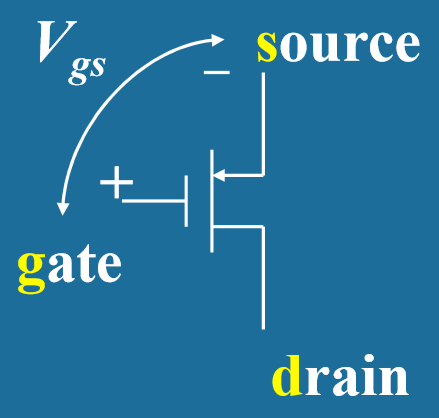
- PMOS晶体管 (P-channel Metal-Oxide-Semiconductor)
- 结构组成:同样包含gate(栅极)、source(源极)、drain(漏极)三个端子
- 工作原理:与NMOS相反,通过栅极电压( Vgs )反向控制source-drain之间的电阻
- 开关特性:
- 当 Vgs = 0 时:PMOS晶体管处于OFF状态, Rds 很大
- 当 Vgs < 0 (低电平)时:PMOS晶体管处于ON状态, Rds 显著降低
- 控制规律: Vgs 减小 → Rds 减小 (Point in - 反向导通)
- CMOS技术优势
- 互补特性:NMOS和PMOS的导通条件互补,可构成完整的逻辑门电路
- 低功耗:静态时总有一个晶体管处于截止状态,几乎无静态功耗
- 高集成度:晶体管可以做得很小,适合大规模集成电路
- 逻辑完备性:可以实现所有基本逻辑运算(AND, OR, NOT)
- CMOS Gate(这里只挑了典型来讲)
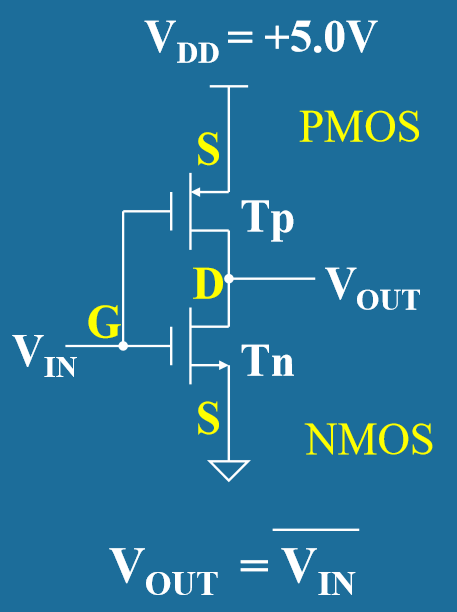
- CMOS反相器 (CMOS Inverter)
- 电路结构:由一个PMOS晶体管和一个NMOS晶体管串联组成
- 工作原理:
- 当输入A为低电平(0)时:PMOS导通,NMOS截止,输出Y为高电平(1)
- 当输入A为高电平(1)时:PMOS截止,NMOS导通,输出Y为低电平(0)
- 逻辑功能: Y = Ā
- 特点:结构简单,功耗低,是CMOS电路的基本单元,相当于非门的逻辑
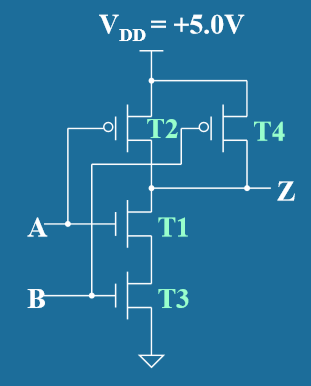
- CMOS与非门 (CMOS NAND Gate)
- 电路结构:由两个PMOS晶体管并联作为上拉网络,两个NMOS晶体管串联作为下拉网络
- 工作原理:
- 当A=0或B=0时:至少有一个PMOS导通,两个NMOS至少有一个截止,输出Y为高电平(1)
- 当A=1且B=1时:两个PMOS都截止,两个NMOS都导通,输出Y为低电平(0)
- 逻辑功能: Y = A·B 的非
- 特点:NAND门是逻辑完备的,可以构造任何逻辑函数
- CMOS缓冲器 (CMOS Buffer)
- 电路结构:由两个反相器级联组成,实现两次反相
- 工作原理:
- 输入信号经过第一个反相器得到反相信号
- 反相信号再经过第二个反相器恢复为原信号
- 逻辑功能: Y = A (同相输出)
- 特点:
- 提供信号放大和驱动能力
- 增强信号的扇出能力
- 改善信号的上升/下降时间
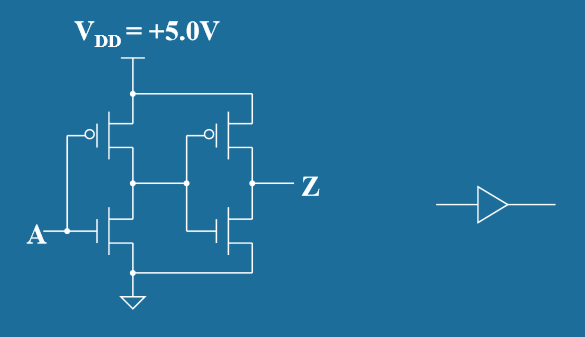
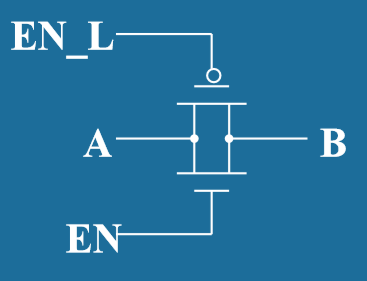
- 传输门 (Transmission Gate)
- 电路结构:由一个NMOS和一个PMOS并联组成,共享输入输出端
- 控制信号:需要一对互补的控制信号C和 C̄
- 工作原理:
- 当C=1, C̄ =0时:两个晶体管都导通,信号可以双向传输
- 当C=0, C̄ =1时:两个晶体管都截止,信号被阻断
- 逻辑功能:可控制的双向开关
- 特点:
- 双向传输特性
- 传输全电平范围的信号
- 常用于多路选择器和存储器
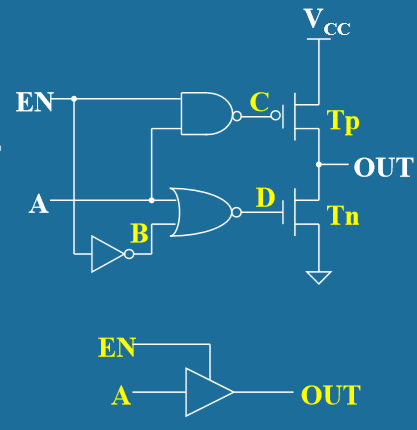
- 三态缓冲器 (Three-state Buffer)
- 电路结构:在普通缓冲器基础上增加使能控制电路
- 三种输出状态:
- 高电平(1):当EN=1且A=1时
- 低电平(0):当EN=1且A=0时
- 高阻态(Z):当EN=0时,输出端相当于断开
- 工作原理:
- 当使能信号EN=1时:电路工作为普通缓冲器
- 当使能信号EN=0时:输出进入高阻抗状态
- 应用场合:
- 总线系统中的信号控制
- 多个输出共享同一条线路
- 需要输出隔离的场合
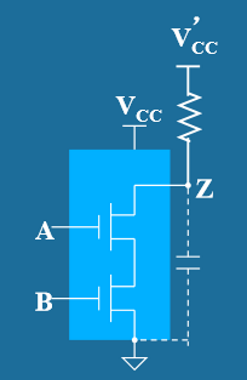
- 开漏输出电路 (Open-Drain Output Circuit)
- 电路结构:只有下拉NMOS晶体管,没有上拉PMOS晶体管的输出结构
- 工作原理:
- 当输入为高电平时:NMOS导通,输出被拉至低电平(0)
- 当输入为低电平时:NMOS截止,输出呈现高阻态,需要外部上拉电阻提供高电平
- 输出特性:
- 低电平:由NMOS晶体管提供强驱动能力
- 高电平:由外部上拉电阻提供,驱动能力较弱
- 应用优势:
- 可实现线与(Wired-AND)逻辑
- 输出电压可以不同于电源电压
- 多个输出可以并联连接
- 适合总线应用和电平转换
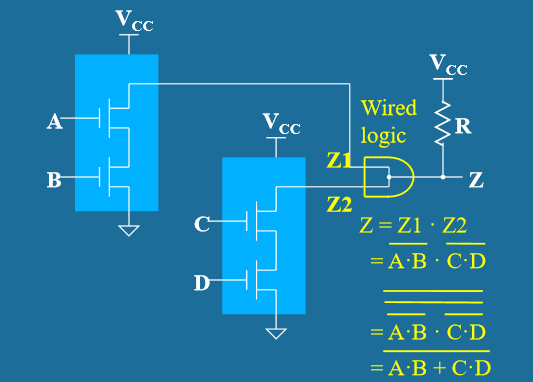
- 线逻辑 (Wired Logic)
- 基本概念:通过直接连接多个门电路的输出端来实现逻辑运算
- 线与逻辑 (Wired-AND):
- 多个开漏输出并联连接,配合上拉电阻
- 只有当所有输出都为高阻态时,总输出才为高电平
- 任何一个输出为低电平时,总输出就为低电平
- 逻辑关系: Y = A₁ · A₂ · A₃ · ... · Aₙ
- 应用场合:
- 总线仲裁电路
- 多设备共享信号线
- 中断请求信号汇总
- 降低连接复杂度
- 注意事项:
- 只能用于开漏或集电极开路输出
- 需要合适的上拉电阻值
- 会增加信号延迟
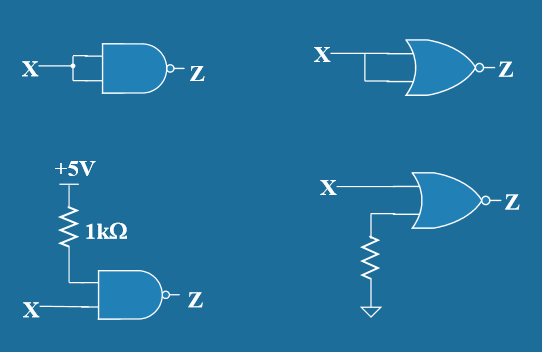
- CMOS电路的未使用输入端处理 (Unused Inputs of CMOS Circuit)
- 问题描述:CMOS门电路的输入端如果悬空,会导致不确定的逻辑状态
- 悬空输入的危害:
- 输入电平不确定,可能在逻辑阈值附近浮动
- 造成输出状态不稳定
- 增加功耗(两个晶体管可能同时部分导通)
- 产生振荡或噪声敏感
- 正确处理方法:
- 接高电平:通过电阻连接到VDD(适用于不影响逻辑的输入)
- 接低电平:通过电阻连接到GND(适用于不影响逻辑的输入)
- 与其他输入并联:连接到已使用的输入端
- 电阻选择:通常使用10kΩ-100kΩ的上拉或下拉电阻
- 设计原则:确保未使用输入不会改变电路的预期逻辑功能
-
Electrical Characteristics
- 扇入 (Fan-in)
- 定义:一个逻辑门能够接受的输入信号的最大数量
- 影响因素:
- 输入阻抗:每个输入端的等效电阻
- 噪声容限:多个输入时的噪声累积效应
- 传输延迟:输入数量增加会影响信号传播时间
- 典型值:
- TTL系列:通常为8-10个输入
- CMOS系列:可达12-16个输入
- ECL系列:通常为4-8个输入
- 设计考虑:扇入过大会降低电路的开关速度和噪声容限
- 扇出 (Fan-out)
- 定义:一个逻辑门输出端能够驱动的同类门电路输入端的最大数量
- 决定因素:
- 输出驱动能力:门电路能提供的最大输出电流
- 输入负载特性:被驱动门电路的输入电流需求
- 电压电平要求:保证逻辑电平的有效性
- 计算公式:
\(\text{扇出} = \min\left(\frac{I_{OL(max)}}{I_{IL(max)}}, \frac{I_{OH(max)}}{I_{IH(max)}}\right)\)
- \(I_{OL}\) :输出低电平时的灌电流能力
- \(I_{OH}\) :输出高电平时的拉电流能力
- \(I_{IL}\) :输入低电平时的漏电流
- \(I_{IH}\) :输入高电平时的输入电流
- 典型扇出值:
- 标准TTL:10
- LS-TTL:20
- HC-CMOS:50-80
- HCT-CMOS:10-20
- 电平兼容性分析
-
逻辑电平定义:
参数 TTL CMOS(5V) CMOS(3.3V) \(V_{IH(min)}\) 2.0V 3.5V 2.0V \(V_{IL(max)}\) 0.8V 1.5V 0.8V \(V_{OH(min)}\) 2.4V 4.4V 2.4V \(V_{OL(max)}\) 0.4V 0.4V 0.4V -
兼容性判断标准:
- 输出高电平 ≥ 输入高电平阈值: \(V_{OH(min)} \geq V_{IH(min)}\)
- 输出低电平 ≤ 输入低电平阈值: \(V_{OL(max)} \leq V_{IL(max)}\)
- 驱动能力满足:扇出计算结果 ≥ 实际负载数量
-
-
74HCT驱动74LS的实例分析
电路特性参数:器件类型 VOH(min) VOL(max) IOH(max) IOL(max) 74HCT 4.4V 0.1V 4mA 4mA 74LS 2.4V 0.5V - - 器件类型 VIH(min) VIL(max) IIH(max) IIL(max) 74HCT 2.0V 0.8V 1µA 1µA 74LS 2.0V 0.8V 20µA 0.4mA </div>
例题计算: - (High-state fanout)高电平扇出: \(\frac{I_{OH}}{I_{IH}}\frac{4mA}{20µA} = 200\) - (Low-state fanout)低电平扇出: \(\frac{I_{OL}}{I_{IL}}=\frac{4mA}{0.4mA} = 10\) - (Overall fanout)实际扇出 = min(200, 10) = 10 - (Residual driving capacity of high state output)剩余驱动力: \(I_{OH}-F_{overall} \times I_{IH}=3.8mA\) 应用优势:
- 74HCT专为TTL兼容而设计,具有TTL电平阈值
- 保持CMOS的低功耗特性
- 实现CMOS到TTL的无缝接口
- 适合混合逻辑系统设计
- 设计注意事项
- 信号完整性:扇出过大会导致信号边沿变缓,影响时序
- 功耗考虑:驱动多个负载会增加动态功耗
- 布线考虑:多个负载需要考虑传输线效应和信号延迟
- 噪声容限:负载增加会降低系统的抗噪声能力
-
直流噪声容限 (Direct Current Noise Margin)
- 定义:数字电路在直流条件下能够容忍的噪声干扰的最大幅度,是衡量电路抗干扰能力的重要指标
- 计算公式:
- 低电平噪声容限: NML = VIL(max) - VOL(max)
- 高电平噪声容限: NMH = VOH(min) - VIH(min)
- 总噪声容限: NM = min(NML, NMH)
- 物理意义:
- NML :在低电平状态下,输入端能承受的最大正向噪声幅度
- NMH :在高电平状态下,输入端能承受的最大负向噪声幅度
- 噪声容限越大,电路的抗干扰能力越强
</div>
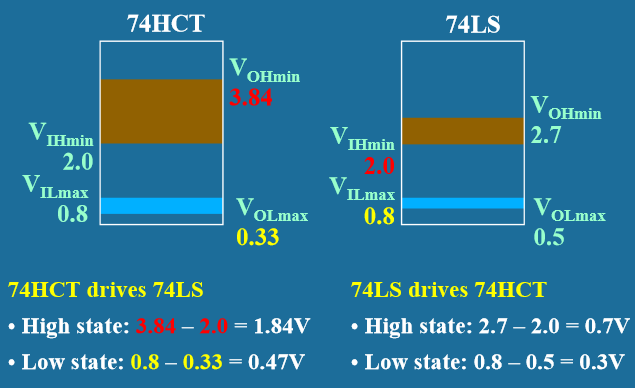
典型电路族的噪声容限对比:
电路族 \(V_{IL(max)}\) \(V_{OL(max)}\) \(NM_L\) \(V_{OH(min)}\) \(V_{IH(min)}\) \(NM_H\) 总噪声容限 CMOS 0.8V 0.33V 0.47V 3.84V 2.0V 1.84V 1.47V TTL 0.8V 0.5V 0.3V 2.7V 2.0V 0.7V 0.3V - 计算
- 扇入 (Fan-in)
Combination
Combination
- Analysis of Combinational Logic Circuit
- 分析组合电路的步骤
- 确定电路的输入和输出
- 识别电路的输入变量(通常用A、B、C等表示)
- 确定电路的输出变量(通常用Y、F等表示)
- 从输入到输出逐级分析
- 从输入端开始,逐级向输出端分析
- 写出每个门电路的逻辑表达式
- 将各级表达式代入,得到最终的逻辑函数
- 化简逻辑函数
- 使用布尔代数定律化简表达式
- 或使用卡诺图进行化简
- 列出真值表
- 根据化简后的逻辑函数
- 列出所有输入组合对应的输出值
- 描述电路功能
- 根据真值表分析电路实现的逻辑功能
- 确定电路的应用场合
- 确定电路的输入和输出
- 分析组合电路的步骤
- Design of Combinational Logic Circuit
- 设计组合电路的步骤
- 问题分析和规格说明
- 明确电路要实现的功能
- 确定输入输出信号的数量和含义
- 定义输入与输出的变量
- 为每个输入信号分配变量名(如A、B、C等)
- 为每个输出信号分配变量名(如Y、F等)
- 定义0与1的状态
- 明确每个变量的逻辑含义
- 例如:A=1表示开关闭合,A=0表示开关断开
- 画真值表
- 列出所有可能的输入组合
- 根据逻辑要求确定每种组合的输出值
- 建立逻辑函数
- 根据真值表写出逻辑函数表达式
- 可以用最小项之和或最大项之积的形式
- 简化逻辑函数
- 使用布尔代数定律或卡诺图化简
- 得到最简的逻辑表达式
- 画电路图
- 根据化简后的逻辑表达式画出电路图
- 选择合适的逻辑门实现电路
- 验证设计
- 检查电路是否满足设计要求
- 进行时序分析和功能验证
- 问题分析和规格说明
- 设计组合电路的步骤
-
Representative Combinational Logic Circuit
常用集成电路器件详解
- 74183 - 全加器 (Full Adder)
- 实际作用:4位二进制全加器,可进行两个4位数的加法运算
- 输入端:
- \(A_3A_2A_1A_0\) :4位被加数
- \(B_3B_2B_1B_0\) :4位加数
- \(C_0\) :最低位进位输入
- 输出端:
- \(\Sigma_3\Sigma_2\Sigma_1\Sigma_0\) :4位和输出
- \(C_4\) :最高位进位输出
- 逻辑表达式:
- \[\Sigma_i = A_i ⊕ B_i ⊕ C_i\]
- \[C_{i+1} = A_iB_i + A_iC_i + B_iC_i\]
- 应用:多位二进制加法运算,可级联实现更多位的加法器
- 74283 - 4位二进制全加器
- 实际作用:与74183功能相同,4位并行二进制全加器
- 输入端:
- \(A_4A_3A_2A_1\) :4位被加数
- \(B_4B_3B_2B_1\) :4位加数
- \(C_0\) :进位输入
- 输出端:
- \(\Sigma_4\Sigma_3\Sigma_2\Sigma_1\) :4位和输出
- \(C_4\) :进位输出
- 真值表(单位举例):
\(A_i\) \(B_i\) \(C_i\) \(\Sigma_i\) \(C_{i+1}\) 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 - 特点:具有超前进位功能,减少传播延迟
- 7485 - 4位数值比较器
- 实际作用:比较两个4位二进制数的大小关系
- 输入端:
- \(A_3A_2A_1A_0\) :4位数据A
- \(B_3B_2B_1B_0\) :4位数据B
- \(I_{A>B}, I_{A=B}, I_{A<B}\) :级联输入端
- 输出端:
- \(O_{A>B}, O_{A=B}, O_{A<B}\) :比较结果输出
- 逻辑表达式:
- \[O_{A>B} = A_3\overline{B_3} + (A_3 ⊙ B_3)A_2\overline{B_2} + (A_3 ⊙ B_3)(A_2 ⊙ B_2)A_1\overline{B_1} + (A_3 ⊙ B_3)(A_2 ⊙ B_2)(A_1 ⊙ B_1)A_0\overline{B_0} + (A_3 ⊙ B_3)(A_2 ⊙ B_2)(A_1 ⊙ B_1)(A_0 ⊙ B_0)I_{A>B}\]
- \[O_{A=B} = (A_3 ⊙ B_3)(A_2 ⊙ B_2)(A_1 ⊙ B_1)(A_0 ⊙ B_0)I_{A=B}\]
- \[O_{A<B} = \overline{A_3}B_3 + (A_3 ⊙ B_3)\overline{A_2}B_2 + (A_3 ⊙ B_3)(A_2 ⊙ B_2)\overline{A_1}B_1 + (A_3 ⊙ B_3)(A_2 ⊙ B_2)(A_1 ⊙ B_1)\overline{A_0}B_0 + (A_3 ⊙ B_3)(A_2 ⊙ B_2)(A_1 ⊙ B_1)(A_0 ⊙ B_0)I_{A<B}\]
- 级联使用:可通过级联输入端连接多个7485实现更多位的比较
- 74LS148 - 8-3线优先编码器
- 实际作用:将8个输入中优先级最高的有效输入编码为3位二进制输出
- 输入端:
- \(\overline{I_7}-\overline{I_0}\) :8个数据输入(低电平有效, \(I_7\) 优先级最高)
- \(\overline{EI}\) :使能输入(低电平有效)
- 输出端:
- \(\overline{A_2}\overline{A_1}\overline{A_0}\) :3位二进制编码输出(低电平有效)
- \(\overline{GS}\) :组选择输出(低电平有效)
- \(\overline{EO}\) :使能输出(低电平有效)
- 真值表:
\(\overline{EI}\) \(\overline{I_7}\) \(\overline{I_6}\) \(\overline{I_5}\) \(\overline{I_4}\) \(\overline{I_3}\) \(\overline{I_2}\) \(\overline{I_1}\) \(\overline{I_0}\) \(\overline{A_2}\) \(\overline{A_1}\) \(\overline{A_0}\) \(\overline{GS}\) \(\overline{EO}\) 1 X X X X X X X X 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 X X X X X X X 0 0 0 0 1 0 1 0 X X X X X X 0 0 1 0 1 0 1 1 0 X X X X X 0 1 0 0 1 0 1 1 1 0 X X X X 0 1 1 0 1 0 1 1 1 1 0 X X X 1 0 0 0 1 0 1 1 1 1 1 0 X X 1 0 1 0 1 0 1 1 1 1 1 1 0 X 1 1 0 0 1 0 1 1 1 1 1 1 1 0 1 1 1 0 1 - 应用:中断优先级编码、键盘扫描、优先级仲裁
- 74LS48 - BCD到七段显示译码器
- 实际作用:将BCD码转换为驱动七段数码管的控制信号
- 输入端:
- \(D_3D_2D_1D_0\) :4位BCD码输入
- \(\overline{LT}\) :灯测试输入(低电平有效)
- \(\overline{RBI}\) :前导零消隐输入(低电平有效)
- \(\overline{BI}\) :消隐输入(低电平有效)
- 输出端:
- \(a,b,c,d,e,f,g\) :七段显示输出(高电平有效)
- \(\overline{RBO}\) :后续零消隐输出(低电平有效)
- 真值表:
\(D_3\) \(D_2\) \(D_1\) \(D_0\) \(\overline{LT}\) \(\overline{RBI}\) \(\overline{BI}\) 显示 a b c d e f g \(\overline{RBO}\) 0 0 0 0 1 1 1 0 1 1 1 1 1 1 0 1 0 0 0 1 1 X 1 1 0 1 1 0 0 0 0 1 0 0 1 0 1 X 1 2 1 1 0 1 1 0 1 1 0 0 1 1 1 X 1 3 1 1 1 1 0 0 1 1 0 1 0 0 1 X 1 4 0 1 1 0 0 1 1 1 0 1 0 1 1 X 1 5 1 0 1 1 0 1 1 1 0 1 1 0 1 X 1 6 1 0 1 1 1 1 1 1 0 1 1 1 1 X 1 7 1 1 1 0 0 0 0 1 1 0 0 0 1 X 1 8 1 1 1 1 1 1 1 1 1 0 0 1 1 X 1 9 1 1 1 1 0 1 1 1 0 0 0 0 1 0 1 灭 0 0 0 0 0 0 0 0 X X X X 0 X 1 8 1 1 1 1 1 1 1 1 X X X X X X 0 灭 0 0 0 0 0 0 0 1 - 特殊功能:
- 前导零消隐: \(\overline{RBI}=0\) 且输入为0000时,显示全灭
- 灯测试: \(\overline{LT}=0\) 时,显示”8”
- 强制消隐: \(\overline{BI}=0\) 时,强制全灭
- 74LS138 - 3-8线译码器
- 实际作用:将3位二进制地址译码为8个输出中的一个
- 输入端:
- \(A_2A_1A_0\) :3位地址输入
- \(\overline{G_{2A}}, \overline{G_{2B}}\) :使能输入(低电平有效)
- \(G_1\) :使能输入(高电平有效)
- 输出端:
- \(\overline{Y_7}-\overline{Y_0}\) :8个译码输出(低电平有效)
- 逻辑表达式:
- 使能条件: \(EN = \overline{G_{2A}} \cdot \overline{G_{2B}} \cdot G_1\)
- \[\overline{Y_i} = \overline{EN \cdot (A_2A_1A_0 = i)}\]
- 真值表:
\(\overline{G_{2A}}\) \(\overline{G_{2B}}\) \(G_1\) \(A_2\) \(A_1\) \(A_0\) \(\overline{Y_7}\) \(\overline{Y_6}\) \(\overline{Y_5}\) \(\overline{Y_4}\) \(\overline{Y_3}\) \(\overline{Y_2}\) \(\overline{Y_1}\) \(\overline{Y_0}\) 1 X X X X X 1 1 1 1 1 1 1 1 X 1 X X X X 1 1 1 1 1 1 1 1 X X 0 X X X 1 1 1 1 1 1 1 1 0 0 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 0 0 1 1 1 1 1 1 1 0 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 1 0 1 1 1 1 0 0 1 1 0 1 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 0 1 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 1 - 应用:地址译码、片选信号产生、存储器译码
- 74LS151 - 8选1数据选择器
- 实际作用:从8路数据输入中选择一路输出
- 输入端:
- \(D_7-D_0\) :8路数据输入
- \(S_2S_1S_0\) :3位选择控制输入
- \(\overline{E}\) :使能输入(低电平有效)
- 输出端:
- \(Y\) :数据输出
- \(\overline{Y}\) :数据输出的反码
- 逻辑表达式:
- \[Y = \overline{E} \cdot (\overline{S_2}\overline{S_1}\overline{S_0}D_0 + \overline{S_2}\overline{S_1}S_0D_1 + \overline{S_2}S_1\overline{S_0}D_2 + \overline{S_2}S_1S_0D_3 + S_2\overline{S_1}\overline{S_0}D_4 + S_2\overline{S_1}S_0D_5 + S_2S_1\overline{S_0}D_6 + S_2S_1S_0D_7)\]
- 真值表:
\(\overline{E}\) \(S_2\) \(S_1\) \(S_0\) Y \(\overline{Y}\) 1 X X X 0 1 0 0 0 0 \(D_0\) \(\overline{D_0}\) 0 0 0 1 \(D_1\) \(\overline{D_1}\) 0 0 1 0 \(D_2\) \(\overline{D_2}\) 0 0 1 1 \(D_3\) \(\overline{D_3}\) 0 1 0 0 \(D_4\) \(\overline{D_4}\) 0 1 0 1 \(D_5\) \(\overline{D_5}\) 0 1 1 0 \(D_6\) \(\overline{D_6}\) 0 1 1 1 \(D_7\) \(\overline{D_7}\) - 应用:数据路由、多路复用、函数发生器
- 74LS153 - 双4选1数据选择器
- 实际作用:包含两个独立的4选1数据选择器
- 输入端:
- 选择器1: \(1D_3, 1D_2, 1D_1, 1D_0\) (数据输入), \(\overline{1G}\) (使能)
- 选择器2: \(2D_3, 2D_2, 2D_1, 2D_0\) (数据输入), \(\overline{2G}\) (使能)
- \(S_1S_0\) :公共选择控制输入
- 输出端:
- \(1Y\) :选择器1输出
- \(2Y\) :选择器2输出
- 逻辑表达式:
- \[1Y = \overline{1G} \cdot (\overline{S_1}\overline{S_0} \cdot 1D_0 + \overline{S_1}S_0 \cdot 1D_1 + S_1\overline{S_0} \cdot 1D_2 + S_1S_0 \cdot 1D_3)\]
- \[2Y = \overline{2G} \cdot (\overline{S_1}\overline{S_0} \cdot 2D_0 + \overline{S_1}S_0 \cdot 2D_1 + S_1\overline{S_0} \cdot 2D_2 + S_1S_0 \cdot 2D_3)\]
- 真值表(单个选择器):
\(\overline{G}\) \(S_1\) \(S_0\) Y 1 X X 0 0 0 0 \(D_0\) 0 0 1 \(D_1\) 0 1 0 \(D_2\) 0 1 1 \(D_3\) - 应用:双路数据选择、时分复用、逻辑函数实现
- 74183 - 全加器 (Full Adder)
- Hazard of Combinational Logic Circuit
- 竞争冒险现象
- 定义:由于门电路传播延迟不同,导致输出出现不期望的瞬态脉冲
- 静态冒险:输出应该保持稳定,但出现瞬态脉冲
- 动态冒险:输出在变化过程中出现多次跳变
- 消除方法
- 增加冗余项
- 使用选通信号
- 改进电路设计
- 竞争冒险现象
-
典型设计实例
例题1:转换8421BCD码成余三码
设计一个将8421BCD码转换为余三码的组合逻辑电路。
解题步骤:
- 列出真值表:
十进制 8421BCD 余三码 0 0000 0011 1 0001 0100 2 0010 0101 3 0011 0110 4 0100 0111 5 0101 1000 6 0110 1001 7 0111 1010 8 1000 1011 9 1001 1100 - 建立逻辑函数(设输入为ABCD,输出为WXYZ):
- \[W = AB + AC + AD + BCD\]
- \[X = \overline{A}B + \overline{A}C + \overline{B}\overline{C} + \overline{A}D\]
- \[Y = \overline{C}D + C\overline{D}\]
- \[Z = \overline{D}\]
- 化简后的表达式:
- \[W = A + B(C + D)\]
- \[X = \overline{A}(B + C + D) + \overline{B}\overline{C}\]
- \[Y = C ⊕ D\]
- \[Z = \overline{D}\]
例题2:转换8421码为格雷码
设计一个将4位8421二进制码转换为格雷码的组合逻辑电路。
解题步骤:
- 列出真值表:
十进制 8421码(ABCD) 格雷码(WXYZ) 0 0000 0000 1 0001 0001 2 0010 0011 3 0011 0010 4 0100 0110 5 0101 0111 6 0110 0101 7 0111 0100 8 1000 1100 9 1001 1101 10 1010 1111 11 1011 1110 12 1100 1010 13 1101 1011 14 1110 1001 15 1111 1000 - 推导逻辑函数:
- \(W = A\) (最高位保持不变)
- \(X = A ⊕ B\) (相邻位异或)
- \[Y = B ⊕ C\]
- \[Z = C ⊕ D\]
- 转换规律:格雷码 = 二进制码的相邻位异或运算
例题3:使用74LS138实现逻辑函数
使用74LS138实现以下4个逻辑函数:
- \[F_1 = \overline{A}C + \overline{A}BC + ABC\]
- \[F_2 = BC + \overline{A} \cdot \overline{B}C\]
- \[F_3 = A + \overline{A}BC\]
- \[F_4 = \overline{A}BC + \overline{B} \cdot C + ABC\]
解题步骤:
- 将函数转换为最小项形式:
- \[F_1 = \overline{A}C + \overline{A}BC + ABC = \overline{A}\overline{B}C + \overline{A}BC + ABC = m_1 + m_3 + m_7\]
- \[F_2 = BC + \overline{A}\overline{B}C = \overline{A}BC + ABC + \overline{A}\overline{B}C = m_1 + m_3 + m_7\]
- \[F_3 = A + \overline{A}BC = ABC + AB\overline{C} + A\overline{B}C + A\overline{B}\overline{C} + \overline{A}BC = m_3 + m_4 + m_5 + m_6 + m_7\]
- \[F_4 = \overline{A}BC + \overline{B}C + ABC = \overline{A}BC + \overline{A}\overline{B}C + A\overline{B}C + ABC = m_1 + m_3 + m_5 + m_7\]
- 74LS138连接方案:
- 输入端: \(A_2A_1A_0 = CBA\)
- 使能端: \(\overline{G_{2A}} = \overline{G_{2B}} = 0\) , \(G_1 = 1\)
- 输出连接:
- \(F_1 = \overline{Y_1} \cdot \overline{Y_3} \cdot \overline{Y_7}\) (需要附加与门)
- \[F_2 = \overline{Y_1} \cdot \overline{Y_3} \cdot \overline{Y_7}\]
- \[F_3 = \overline{Y_3} \cdot \overline{Y_4} \cdot \overline{Y_5} \cdot \overline{Y_6} \cdot \overline{Y_7}\]
- \[F_4 = \overline{Y_1} \cdot \overline{Y_3} \cdot \overline{Y_5} \cdot \overline{Y_7}\]
例题4:使用4-1数据选择器实现逻辑函数
使用4-1数据选择器实现: \(Y = A\overline{B} \cdot \overline{C} + \overline{A} \cdot \overline{C} + BC\)
解题步骤:
-
选择控制变量:选择AB作为选择信号 \(S_1S_0\)
-
按AB的值分组列出真值表:
A B C Y AB组合 0 0 0 1 00 0 0 1 1 00 0 1 0 0 01 0 1 1 1 01 1 0 0 1 10 1 0 1 0 10 1 1 0 0 11 1 1 1 1 11 - 确定数据输入:
- 当AB=00时: \(Y = 1\) (恒为1) → \(D_0 = 1\)
- 当AB=01时: \(Y = C\) → \(D_1 = C\)
- 当AB=10时: \(Y = \overline{C}\) → \(D_2 = \overline{C}\)
- 当AB=11时: \(Y = C\) → \(D_3 = C\)
- 连接方案:
- 选择信号: \(S_1 = A\) , \(S_0 = B\)
- 数据输入: \(D_0 = 1\) , \(D_1 = C\) , \(D_2 = \overline{C}\) , \(D_3 = C\)
例题5:使用双4-1数据选择器实现多输出函数
使用双4-1数据选择器实现:
- \[F_1(A,B,C,D) = \sum m(0,1,5,7,10,13,15)\]
- \[F_2(A,B,C,D) = \sum m(8,10,12,13,15)\]
解题步骤:
-
选择控制变量:选择AB作为公共选择信号 \(S_1S_0\)
-
**按AB分组分析 \(F_1\) **:
AB CD组合 \(F_1\) 值 对应函数 00 00,01 1,1 \(F_1 = 1\) 01 01,11 1,1 \(F_1 = \overline{C} \cdot D + C \cdot D = D\) 10 10,11 1,0 \(F_1 = \overline{C} \cdot \overline{D}\) 11 01,11 1,1 \(F_1 = \overline{C} \cdot D + C \cdot D = D\) - **按AB分组分析 \(F_2\) **:
AB CD组合 \(F_2\) 值 对应函数 00 XX 0,0 \(F_2 = 0\) 01 XX 0,0 \(F_2 = 0\) 10 00,10 1,1 \(F_2 = \overline{D}\) 11 01,11 1,1 \(F_2 = \overline{C} \cdot D + C \cdot D = D\) - 74LS153连接方案:
- 公共选择信号: \(S_1 = A\) , \(S_0 = B\)
- 选择器1(实现 \(F_1\) ):
- \(1D_0 = 1\) , \(1D_1 = D\) , \(1D_2 = \overline{C} \cdot \overline{D}\) , \(1D_3 = D\)
- 选择器2(实现 \(F_2\) ):
- \(2D_0 = 0\) , \(2D_1 = 0\) , \(2D_2 = \overline{D}\) , \(2D_3 = D\)
Flip-Flop
- \(2D_0 = 0\) , \(2D_1 = 0\) , \(2D_2 = \overline{D}\) , \(2D_3 = D\)
-
Definition of Flip-Flop
触发器基本概念
- 定义:触发器是一种具有记忆功能的双稳态时序逻辑电路,能够存储1位二进制信息
- 基本特性:
- 双稳态特性:具有两个稳定的输出状态(0和1)
- 记忆功能:能够保持当前状态直到控制信号改变
- 时序性:输出不仅取决于当前输入,还取决于电路的历史状态
- 分类方式:
- 按功能:R-S触发器、D触发器、J-K触发器、T触发器
- 按触发方式:电平触发、边沿触发
- 按结构:基本触发器、时钟控制触发器、主从触发器
- 应用领域:
- 数据存储和寄存器
- 计数器和分频器
- 状态机和控制电路
- 时序逻辑系统
- R-S Flip-Flop
- 基本R-S触发器 (Basic R-S Latch)
- 电路结构:由两个交叉耦合的NOR门或NAND门构成
- 输入端:
- R (Reset):复位输入,用于将输出置0
- S (Set):置位输入,用于将输出置1
- 输出端:
- Q:正输出
- Q̄ :反输出(通常与Q互补)
- 工作原理:
- 利用正反馈实现双稳态特性
- 当一个输出为1时,会维持另一个输出为0
- 特点:
- 最基本的存储单元
- 异步工作,立即响应输入变化
- 存在禁止状态
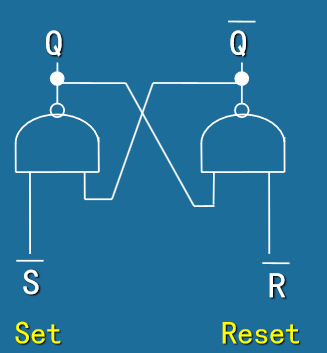
-
基本R-S触发器真值表(NOR门实现):
R S \(Q_{n+1}\) \(\overline{Q_{n+1}}\) 说明 0 0 \(Q_n\) \(\overline{Q_n}\) 保持状态 0 1 1 0 置位(Set) 1 0 0 1 复位(Reset) 1 1 0 0 禁止状态 -
门控R-S锁存器 (Gated R-S Latch)
- 改进设计:在基本R-S触发器基础上增加时钟控制
- 输入端:
- R, S:数据输入端
- CLK (Clock):时钟控制信号
- 工作原理:
- 只有当CLK=1时,R和S信号才能影响输出
- 当CLK=0时,触发器保持当前状态
- 优势:
- 提供时钟同步控制
- 避免异步变化带来的干扰
- 为同步时序电路奠定基础
- 应用:
- 需要同步控制的存储电路
- 作为其他复杂触发器的基础单元
_R-S_Latch.png)
-
门控R-S锁存器真值表:
CLK R S \(Q_{n+1}\) 说明 0 X X \(Q_n\) 保持状态 1 0 0 \(Q_n\) 保持状态 1 0 1 1 置位 1 1 0 0 复位 1 1 1 ? 禁止状态 -
主从R-S触发器 (Master-Slave R-S Flip-Flop)
- 结构组成:由两级门控R-S锁存器串联构成
- 主锁存器(Master):接收输入信号
- 从锁存器(Slave):控制最终输出
- 时钟控制:
- 主锁存器在CLK=1时工作
- 从锁存器在CLK=0时工作
- 工作过程:
- 上升沿:数据进入主锁存器
- 高电平期间:主锁存器可能多次变化
- 下降沿:主锁存器状态传递给从锁存器
- 特点:
- 在时钟下降沿改变输出状态
- 避免了电平触发的空翻问题
- 输出变化与输入变化在时间上分离
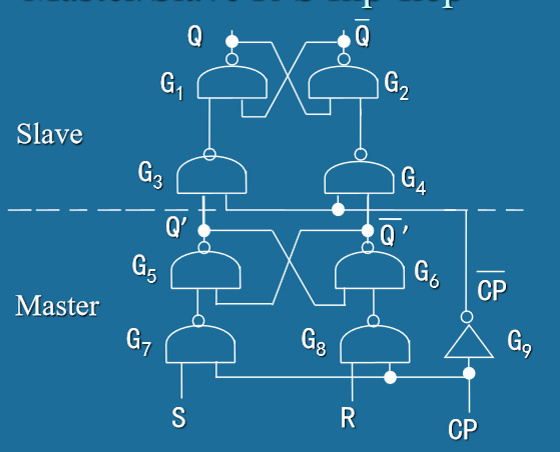
-
主从R-S触发器工作时序:
时钟状态 主锁存器 从锁存器 输出Q CLK上升沿 接收R,S 保持 不变 CLK=1期间 跟随R,S 保持 不变 CLK下降沿 保持 接收主锁存器状态 改变 CLK=0期间 保持 保持 稳定
- D Flip-Flop
- 门控D锁存器 (Gated D Latch)
- 设计思想:为解决R-S触发器的禁止状态问题而设计
- 电路结构:在门控R-S锁存器的R输入端增加反相器
- 输入端:
- D (Data):数据输入端
- CLK:时钟控制信号
- 内部连接:
- S = D
- R = D̄
- 功能特点:
- 无禁止状态,任何时候R和S不会同时为1
- 输出跟随输入:Q = D(当CLK=1时)
- 简化了控制逻辑
- 应用优势:
- 数据寄存器的基本单元
- 流水线系统中的数据缓存
- 同步数据传输
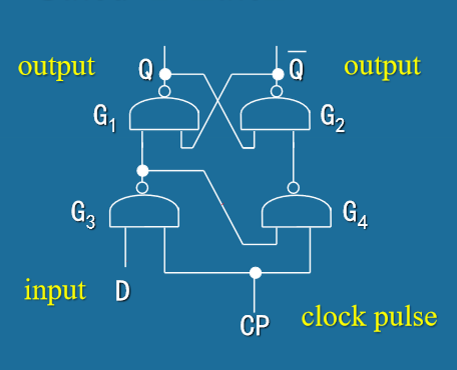
-
门控D锁存器真值表:
CLK D \(Q_{n+1}\) 说明 0 X \(Q_n\) 保持状态 1 0 0 输出跟随输入 1 1 1 输出跟随输入 -
上升沿触发D触发器 (Rising-edge Triggered D Flip-Flop)
- 触发方式:在时钟上升沿瞬间改变输出状态
- 电路实现:
- 方法1:主从结构 + 边沿检测电路
- 方法2:传输门结构
- 方法3:CMOS开关电路
- 工作特点:
- 只在CLK上升沿响应D输入
- 其他时间输出保持不变
- 避免了透明锁存器的竞争冒险
- 时序参数:
- 建立时间(Setup Time):CLK边沿前D必须稳定的时间
- 保持时间(Hold Time):CLK边沿后D必须保持的时间
- 传播延迟(Propagation Delay):从CLK边沿到Q变化的时间
- 设计优势:
- 时序控制精确
- 抗干扰能力强
- 便于级联使用
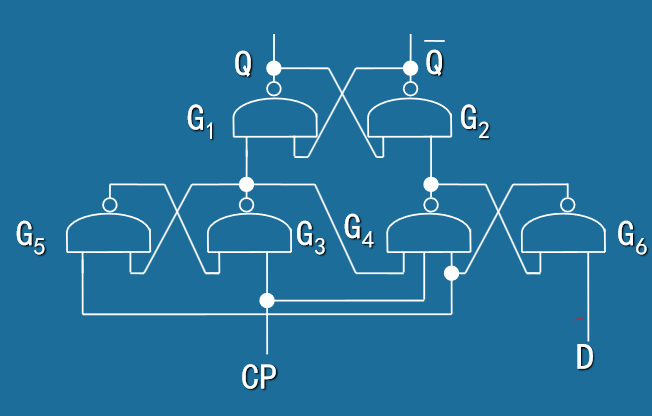
-
边沿触发D触发器特性表:
CLK D \(Q_{n+1}\) 说明 ↑ 0 0 上升沿触发,Q=D ↑ 1 1 上升沿触发,Q=D 0,1,↓ X \(Q_n\) 非上升沿时保持
- J-K Flip-Flop
- 门控J-K锁存器 (Gated J-K Latch)
- 设计改进:在门控R-S锁存器基础上解决禁止状态问题
- 输入端:
- J (Jump):类似于S输入,置位功能
- K (Kill):类似于R输入,复位功能
- CLK:时钟控制信号
- 反馈连接:
- J输入端增加 Q̄ 反馈
- K输入端增加Q反馈
- 功能特点:
- J=K=1时实现翻转功能,无禁止状态
- 具有R-S触发器的所有功能
- 增加了翻转(Toggle)功能
- 逻辑方程:
- Qn+1 = JQ̄n + K̄Qn
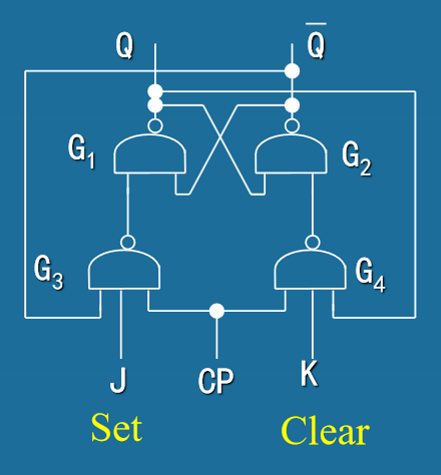
-
J-K锁存器真值表:
CLK J K \(Q_{n+1}\) 说明 0 X X \(Q_n\) 保持状态 1 0 0 \(Q_n\) 保持状态 1 0 1 0 复位 1 1 0 1 置位 1 1 1 \(\overline{Q_n}\) 翻转 -
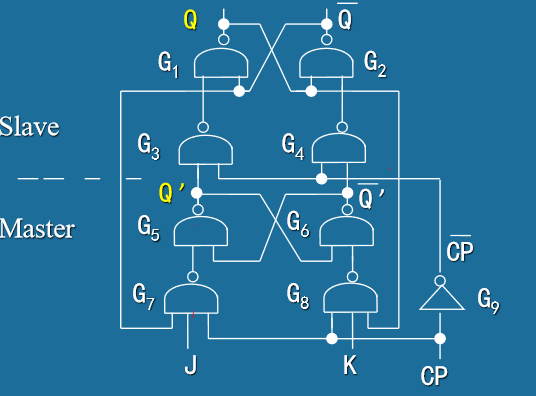
主从J-K触发器 (Master-Slave J-K Flip-Flop)
- 结构特点:采用主从结构避免空翻现象
- 工作原理:
- 主级在CLK=1时接收J、K输入
- 从级在CLK=0时接收主级输出
- 在CLK下降沿改变最终输出
- 解决问题:
- 消除了门控J-K锁存器的空翻问题
- 提供稳定的翻转功能
- 实现可预测的时序行为
- 应用领域:
- 计数器设计
- 频率分频电路
- 状态机实现
- 设计考虑:
- 1s捕获问题:CLK=1期间输入变化会影响结果
- 需要严格的时序设计
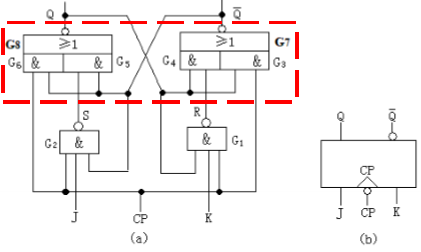
- 边沿触发J-K触发器 (Edge-Triggered J-K Flip-Flop)
- 触发方式:在时钟边沿瞬间采样J、K输入
- 优势特点:
- 只在时钟边沿响应输入变化
- 避免了主从触发器的1s捕获问题
- 具有更好的抗干扰特性
- 时序要求:
- 建立时间:边沿前输入必须稳定
- 保持时间:边沿后输入必须保持
- 功能完整性:
- 保持、置位、复位、翻转四种功能
- 是最通用的触发器类型
- 现代应用:
- 高速数字系统首选
- 同步电路设计标准
-
边沿触发J-K触发器特性表:
CLK J K \(Q_{n+1}\) 功能 ↑ 0 0 \(Q_n\) 保持 ↑ 0 1 0 复位 ↑ 1 0 1 置位 ↑ 1 1 \(\overline{Q_n}\) 翻转 其他 X X \(Q_n\) 保持
- Integrated Flip-Flop
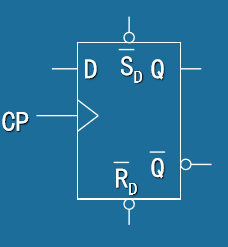
- 集成D触发器 (Integrated D Flip-Flop)
- 典型器件:74LS74、74HC74等
- 引脚功能:
- D:数据输入端
- CLK:时钟输入端(上升沿触发)
- P̄R :异步预置端(低电平有效)
- C̄LR :异步清零端(低电平有效)
- Q:正输出端
- Q̄ :反输出端
- 异步功能:
- 预置: P̄R=0 时,Q立即置1
- 清零: C̄LR=0 时,Q立即置0
- 异步功能优先级高于同步功能
- 应用特点:
- 工业标准器件
- 可靠性高,使用方便
- 适合大规模集成应用
-
集成D触发器完整功能表:
\(\overline{PR}\) \(\overline{CLR}\) CLK D Q \(\overline{Q}\) 说明 0 1 X X 1 0 异步预置 1 0 X X 0 1 异步清零 0 0 X X 1 1 禁用状态 1 1 ↑ 0 0 1 同步清零 1 1 ↑ 1 1 0 同步置位 1 1 其他 X \(Q_n\) \(\overline{Q_n}\) 保持状态 -
集成J-K触发器 (Integrated J-K Flip-Flop)
- 典型器件:74LS76、74HC76等
- 引脚配置:
- J、K:数据输入端
- CLK:时钟输入端
- P̄R :异步预置端
- C̄LR :异步清零端
- Q、 Q̄ :输出端
- 功能完备性:
- 包含所有基本逻辑功能
- 异步和同步控制并存
- 灵活的控制方式
- 设计优势:
- 通用性强,适应性好
- 可实现复杂的时序逻辑
- 是构建复杂数字系统的基础

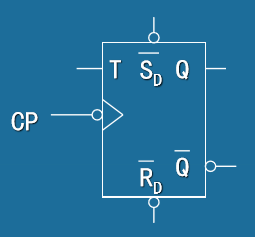
- 集成T触发器 (Integrated T Flip-Flop)
- 实现方式:通常由J-K触发器连接而成(J=K=T)
- 输入端:
- T (Toggle):翻转控制输入
- CLK:时钟输入
- 功能特点:
- T=0时保持当前状态
- T=1时在时钟边沿翻转状态
- 专门用于计数和分频应用
- 逻辑方程:
- Qn+1 = TQ̄n + T̄Qn = T ⊕ Qn
- 典型应用:
- 二进制计数器
-
T触发器特性表:
CLK T \(Q_{n+1}\) 说明 ↑ 0 \(Q_n\) 保持状态 ↑ 1 \(\overline{Q_n}\) 翻转状态 其他 X \(Q_n\) 保持状态
- Conversion Between Flip-Flop
-
触发器类型转换原理
触发器之间的转换是通过在目标触发器的输入端增加适当的组合逻辑电路来实现的。转换的核心是使目标触发器的特性表与所需触发器的特性表相匹配。
-
D触发器转换为其他类型
目标类型 转换电路 逻辑表达式 说明 T触发器 D = T⊕Q \(D = T \oplus Q_n\) T=1时翻转,T=0时保持 J-K触发器 D = JQ̄+K̄Q \(D = J\overline{Q_n} + \overline{K}Q_n\) 实现J-K的完整功能 R-S触发器 D = S+R̄Q \(D = S + \overline{R}Q_n\) S置位,R复位 J-K触发器转换为其他类型
目标类型 转换电路 逻辑表达式 说明 D触发器 J=D, K=D̄ \(J = D, K = \overline{D}\) 最简单的转换 T触发器 J=T, K=T \(J = K = T\) 直接连接实现 R-S触发器 J=S, K=R \(J = S, K = R\) 功能对应关系 -
转换设计步骤:
- 列出目标触发器的特性表
- 列出现有触发器的特性表
- 建立转换真值表
- 设计输入逻辑电路
- 验证转换正确性
-
转换实例:D触发器实现J-K功能
\(Q_n\) J K \(Q_{n+1}\) D 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 0 0 1 1 0 1 1 1 1 1 0 0 -
卡诺图化简得到: \(D = J\overline{Q_n} + \overline{K}Q_n\)
-
触发器选择指南:
应用场合 推荐类型 原因 数据寄存器 D触发器 输入输出关系简单明确 计数器 J-K或T触发器 具有翻转功能 状态机 D或J-K触发器 功能全面,控制灵活 分频器 T触发器 专门的翻转功能 移位寄存器 D触发器 数据传输简单可靠